Het Vermoeden van Collatz
- Geej se lèllike voel hod!
- We're not arrogant, we just think we're the best band in the world ~ Noel Gallagher
- Schaamplipverkleiningen en andere genitale chirurgie zitten in de lift
- Aunt Bunt Cunt
- jezus zei tegen god, ik ben van de pot
- De verdachte had als alibi dat hij op het moment van het misdrijf in Sint-Gillis-Waas
- ...dat is als gorgelen met snot
- Ik doe geen vlieg kwaad - I do no fly angry
- Ᵹoed ᵹedaan.
- Dat bakkes van jou, kan dat ook dicht? Doe eens?
- Waarom moet Clucht Brugge eigenlijk altijd (ex-)spelers van Genk binnenhalen? Hebben zij zelf geen scouting-unit?
- 't Is niet dat ik je haat of zo, maar fuck gewoon off
- Seg, mag kik na ok es iet vraoge?
- Sorry voor de ironie, maar wat 'n GEKLÁÁÁÁÁÁÁÁÁÁÁÁÁÁGGGGG toch weer op facebook!!!
- Jij bent ZO DIK, dat er een uur verschil zit tussen je navel en je ruggegraat
- Verknoei je tijd op een nuttige manier!
Wiskunde is tof!
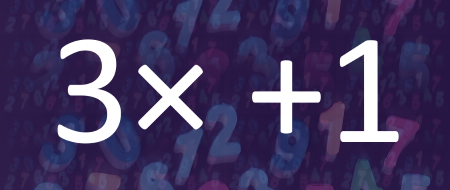
De Duitse wiskundige Lothar Collatz bedacht in 1937 deze mysterieuze getaltheorie, waarbij ongeacht welk startgetal je neemt, de volledige berekening altijd op 1 uitkomt.
De volgende formule wordt gehanteerd: als je startgetal onpaar is wordt dit met 3 vermenigvuldigd en wordt er 1 bijgeteld. Is het getal paar, dan wordt het door 2 gedeeld. Deze formule herhaalt zichzelf tot men op 1 uitkomt.
Volgens Collatz is het niet mogelijk om niet op 1 uit te komen.
Zoals elders vermeld op deze site zijn we eropuit om te proberen allerhande berekeningen, formules, spelletjes en andere dingen in scriptjes te gieten. We zijn er, na niet zo lang klooien en prutsen, uit geraakt. Ongetwijfeld zal er wel een accuratere manier zijn om dit uit te voeren maar we zijn maar hobbyisten en autodidact programmeurs. Het werkt en dat is wat telt!
Het getal wat tot nu toe het dichtst bij het eigen aantal berekeningen ligt, is 19, met 20 stappen.
Laat de magie gebeuren!
Geef in onderstaand formuliertje een getal naar keuze in en Eluterius berekent de hele trip naar het cijfer 1.Statistiekjes... yeah!!
Er zijn reeds 831 startgetallen ingegeven. We kunnen nu natuurlijk allerlei dingen doen met de statistiekjes en berekeningen. Zoals bijvoorbeeld de startgetallen groeperen per aantal stappen. Deze lijst toont de 50 meest voorkomende reeksen van stappen, met de getallen die deze stappen genereren erbij, en het aantal keren dat dit aantal stappen gegenereerd werd. Er zijn tot nu toe 209 verschillende aantal stappen gegenereerd. Het laagst aantal stappen is 1, het hoogst is 567.
STARTGETAL
×
30
86, 87, 89, 520, 522, 524, 525, 528, 529, 532, 533, 536, 538, 555, 571, 577, 578, 579, 583, 633, 635, 20000,
22
28
130, 131, 132, 133, 134, 788, 789, 792, 794, 800, 808, 810, 866, 867, 868, 869, 883, 950, 951, 955, 5005,
21
25
98, 99, 100, 101, 102, 576, 592, 596, 597, 642, 643, 648, 650, 652, 653, 713,
16
36
153, 156, 157, 158, 912, 916, 917, 920, 922, 930, 931, 948, 952, 971, 1025,
15
118
97, 580, 581, 582, 584, 586, 587, 588, 589, 123555, 744556, 756423, 797997, 4807772, 26082023,
15
129
913, 914, 915, 918, 919, 921, 924, 925, 926, 929, 935, 940, 959, 42424242,
14
22
72, 74, 76, 77, 81, 480, 482, 483, 488, 490, 497, 534, 535, 537,
14
39
203, 209, 210, 211, 1224, 1256, 1265, 7445, 7468, 7552, 7896, 9004, 9005, 9006,
14
20
18, 19, 112, 116, 117, 120, 122, 720, 744, 753, 802, 804, 806,
13
23
25, 144, 148, 149, 152, 154, 162, 163, 928, 936, 938, 960, 964,
13
126
684, 685, 686, 689, 690, 691, 694, 695, 697, 707, 25000, 855855,
12
48
481, 489, 492, 493, 494, 498, 499, 508, 509, 510, 539, 3000,
12
33
114, 118, 119, 688, 692, 693, 696, 698, 710, 712, 777, 4444,
12
43
540, 541, 542, 545, 551, 556, 557, 574, 575, 606, 20202, 22000,
12
15
22, 23, 136, 138, 140, 141, 150, 151, 832, 904, 909,
11
21
36, 37, 38, 224, 232, 234, 240, 241, 244, 245, 8960,
11
56
569, 585, 590, 591, 601, 636, 637, 638, 3600, 23000, 745698,
11
31
172, 173, 174, 177, 178, 179, 1111, 1266, 1267, 40000, 45889,
11
17
14, 15, 88, 90, 92, 93, 544, 552, 554, 602,
10
38
105, 631, 632, 634, 647, 683, 687, 3950, 4111, 150922,
10
26
33, 196, 197, 198, 200, 202, 204, 205, 217, 8552,
10
18
28, 29, 30, 176, 180, 181, 184, 186, 201,
9
51
641, 657, 658, 659, 676, 677, 678, 718, 719,
9
27
65, 66, 67, 400, 404, 405, 408, 410, 433,
9
41
135, 139, 812, 813, 818, 844, 910, 911, 6006,
9
113
108, 109, 110, 656, 660, 666, 674, 675, 4000,
9
12
17, 96, 104, 106, 113, 640, 672, 680, 682,
9
19
9, 56, 58, 60, 61, 369, 401, 402, 403,
9
116
145, 146, 147, 872, 884, 885, 899, 903, 927,
9
54
159, 855, 877, 900, 901, 902, 956, 957,
8
14
11, 68, 69, 70, 75, 426, 452, 453,
8
123
514, 515, 516, 517, 518, 521, 530, 531,
8
13
34, 35, 192, 208, 212, 213, 226, 227,
8
34
39, 228, 229, 230, 236, 237, 238,
7
40
406, 407, 409, 420, 421, 422, 455,
7
35
78, 79, 456, 458, 477, 507, 513,
7
61
505, 511, 519, 566, 567, 123456, 680777,
7
110
82, 83, 496, 500, 501, 504, 506,
7
111
27, 164, 166, 1000, 6174, 1234567, 1255555,
7
44
185, 187, 191, 1212, 8002, 8030, 40404,
7
64
673, 679, 681, 699, 711, 755,
6
9
12, 13, 80, 84, 85, 512,
6
16
7, 44, 45, 46, 301, 302,
6
105
94, 95, 568, 570, 572, 573,
6
100
107, 644, 645, 646, 651, 808080,
6
49
169, 963, 986, 988, 999, 5899,
6
72
799, 888, 892, 4785, 5366, 5369,
6
46
123, 127, 735, 764, 809, 4597,
6
120
399, 2344, 14144, 85546, 86552, 88996,
6
114
216, 218, 220, 221, 8000, 45896,
6
Er kan nog meer met deze gegevens gedaan worden.
We kunnen al stellen dat een groter startgetal niet altijd automatisch een groter aantal stappen genereert. En dat er regelmatig drie of vijf opeenvolgende getallen, een gelijk aantal stappen genereren. Zie grafiekje:
Startgetal
Aantal stappen
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
Dit zijn 50 berekeningen van de ingegeven 831 getallen. Om de hele lijst te zien klik hier.
Links
Rechts